【提携サイト】広告サイトではありません↓
管理人の「わお&なお」様より当サイトに漫画・イラスト等を提供いただいています。
1.ベクトルの掛け算ってあるの?
ベクトルの和,差というものは知っていますか?
高校数学で学習しますし,説明されればきちんと納得のいく定義です。
ベクトルの和は,「2つの移動量の合計」と考えることができます。右上にa→だけ移動し,引き続き右下にb→だけ移動した場合,要するに合わせていくら移動したのかは右の図のような矢印「a→+b→」で表されますね。これがベクトルの和です。
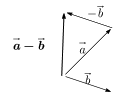 ベクトルの差は,「逆ベクトルとの和」と考えると分かりやすいでしょう。右の図のように,b→と大きさが同じで向きが逆のベクトル「-b→」を考え,それとの和を作れば「a→-b→」を表すことができます。
ベクトルの差は,「逆ベクトルとの和」と考えると分かりやすいでしょう。右の図のように,b→と大きさが同じで向きが逆のベクトル「-b→」を考え,それとの和を作れば「a→-b→」を表すことができます。
つまり,ベクトルには足し算と引き算があることになります。これに実数倍という発想も加えると,
a→+2b→ とか,2(a→+3b→)=2a→+6b→ といったように,普通の文字式と同じような感覚で「矢印」という図形を「計算」することができるのです。
ところが,何もかも文字式と同じかというとそうではありません。
文字式の計算にはあって,ベクトルの計算にはないものがあります。
掛け算です。
「ベクトルの内積があるじゃないですか」
という方がいらっしゃるかも知れませんが,内積の場合ベクトルとベクトルを「掛け」ているのに答えがベクトルではなくて実数になります。
(例) a→・b→=3
ベクトルの掛け算というからには,ベクトルとベクトルを掛けたとき,答えもベクトルになってほしいものです。
「外積って言うのがありますよ!」
と,高校数学以上のことをご存じの方は言われるかもしれませんね。確かに外積なら,ベクトルとベクトルを「掛け」た答えもベクトルになります。
しかし外積の場合は,平面ベクトル同士を掛けているのに,答えが空間ベクトルになってしまいます。考えている次元よりも,答えが1つ高い次元になってしまうのが外積です。欲を言えば,平面ベクトルの積は平面ベクトルになって欲しいです。
こういう厳しい目で見ると,ベクトルに「積」というものはありません。
いや,正しくは,「有名ではない」というべきでしょうか。色々な数学書を読んでみても,真のベクトルの積と呼べるものは載っていませんが,定義することは可能なのです。
2.ベクトルの掛け算のカギを握るのは複素数?
ベクトルの積と認められるための条件をもう一度整理しておくと,
① 答えがベクトルになり,
② かつ,平面ベクトルの積は平面ベクトルになること。
でした。この条件を満たす最も身近なものが,実は意外なところに隠されているのです。
複素数です。
まずは
a→=(1,3),b→=(2,2)
のように,ベクトルを成分で表します。これを複素数だと思って,
a=1+3i,b=2+2i
と読み替えてください。この2つの複素数の掛け算は,
(1+3i)(2+2i)=2+2i+6i-6=-4+8i
となります。これを再びベクトルとして読み替えると(-4,8)となりますが・・・
実はこれがベクトルの積の計算方法なのです。
a→×b→=(1,3)×(2,2)=(-4,8)
というのが正解です。
どうしてこれがベクトルの積になるのか,ということが詳しく知りたい方は,私の拙論をご覧いただくとして,色々な条件で厳しく絞り込んでいくと,ベクトルの積には複素数の積が相応しいことがいえるのです。
ベクトルの掛け算があるということは,その逆である割り算も決めることができるわけです。
こういう言い方もできます。
「ベクトルには足し算,掛け算がある。もし掛け算と割り算があるのならば,ベクトルはまるで数であるかのように四則演算ができることになる。実はこうやって四則演算ができるようになったベクトルこそ,複素数の正体なのである」
複素数と平面ベクトルの密接な関係は,高校数学であまり語られることはありません。
しかし,ベクトルの積という不思議な演算から複素数が見えること,逆に複素数という「わざとらしく作られた」ような数が,実はベクトルというちゃんとした実体を持っていることなど,面白い関係だと思いませんか?




コメント