お客さんが来て,お土産にケーキを買ってきてくれたとします。
美味しそうなショートケーキで,子どもたちが箱を開け,数を数えてみると「6個ある!」とか「4個ある!」とか騒ぎます。場合によって個数は違うでしょうね。
遅く帰ってきたお父さん。ケーキの箱があるのに気付き,開けてみたらもう既に子どもたちが食べてしまっていて空っぽ。ここで,
「お?ケーキが0個ある(笑)」
なんて冷静に言えるお父さんがいるでしょうか?
普通は「何も入ってないじゃないか!」と言いますよね。
ちょっと想像していただきたいのですが,数字を扱うお仕事をしている方を除き,常日頃の何気ない生活の中で「ゼロ」という言葉を使う機会がありますか?
例えばお休みでゆっくりしているとき,自宅で家事をしているとき,外に遊びに行ったとき,友人と何気ない会話をしているとき…
今日1日で,(数字を扱う業務以外で)何回「ゼロ」という言葉を口にされましたか?
「楽しいこと全然ないな~」
と言うことはあっても,
「楽しいことがゼロ個あるな~」
と言うことなんて,ほとんどないのではありませんか?
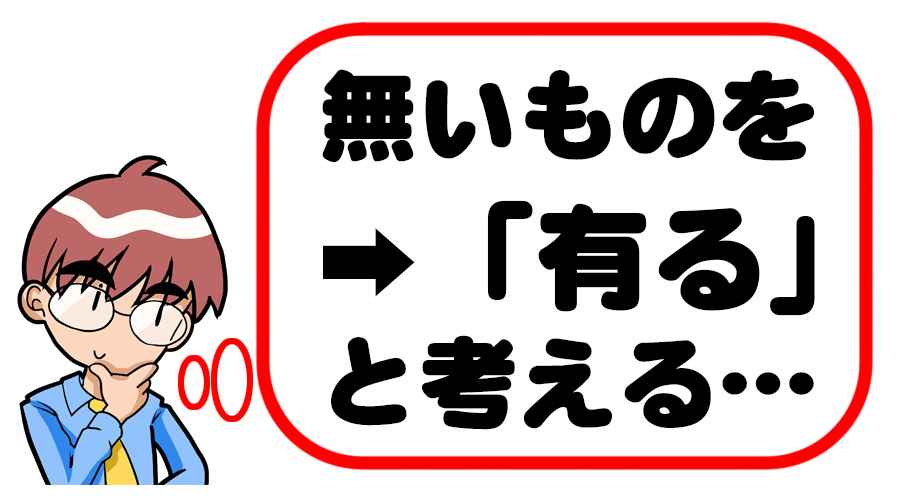
「何もない」ということを「0個ある」と言い換えることが,どれだけ大きな発想の転換かお分かりいただけるでしょうか。
人間の歴史は古いですが,この「0」という発想が誕生するまでには長い年月がかかっていることはあまり知られていません。
「0」という数は人類が初めて自分たちの頭の中で作り上げた数と言ってもいいでしょう。
この数が発明されたことによって,数学は大きな進歩を遂げることができました。いわば,数学史上の大発明なのです。
はるか昔,人間にとって「自然数」が数の全てでした。
羊が4匹いる,石ころが7個ある,木が10本生えている,といった自然界の個数から1,2,3,4,・・・という数を使うようになっていったといわれています。
その後,半端な数や分配を表すのに「分数(有理数)」が使われるようになりましたが,いずれにしても身の回りにあるものをターゲットにして数を用いていましたので,
「羊の肉を1/3匹分」
とか
「水をこの入れ物の2/3だけ」
とかいう風に,現実に置き換えられる数ばかりが使われていたわけです。
木が一本も生えていない状態は,人間にとってただ「何もない」状態であって,数を用いるターゲットではありませんでした。
だから,昔の人間は「0」という数を必要としなかったのです。
ローマ数字をご存知ですか? 洋風の時計の文字盤によく使われていますが,Ⅰ,Ⅱ,Ⅲ,Ⅳ・・・という記号で表される数字です。
5は「V」,10は「X」,50は「L」,100は「C」という風に記号が決められていて,大きな数はこれらの記号を寄せ集めて表します。
例えば32は「XXXII」,362は「CCCLXII」といった具合です。
0にあたる記号はありません。108のように途中に0がある場合も「CVIII」と寄せ集めて表現するだけですから,0を必要としないわけです。
ところがこの数字,計算をするときにはとても不便なのです。
37+68を考えてみましょう。
ローマ数字なら「XXXVII + LXVIII」とかけます。
記号を全部寄せ集めると「LXXXXVVIIIII」となりますが,ある程度の束になると記号は置き換えていきますから,
「IIIII」→「V」
「VV」→「X」
という置き換えをして「LXXXXXV」。さらに
「XXXXX」→「L」
と置き換えて「LLV」。さらにまた
「LL」→「C」
と置き換えて「CV」。やっと終わって答えは105です。
というように,計算しているというよりは記号の置き換えパズルに時間のほとんどを費やします。
ただの2桁の数の足し算でこれです。桁が大きくなったり,引き算や掛け算,割り算をすること考えてみてください。気が遠くなる作業が必要です。
ヨーロッパの人々も,この数が計算に不向きなことに気がついていて,様々な工夫をしています。
「計算盤」という道具が開発され,あらゆる数を「C」が3個,「L」が1個,「X」が4個,「I」が2個という風に整理して玉を置くようにしました。
「X」が一つもないような数の場合,計算盤の「X」の枠には玉が置かれませんでした。
この状態を「0」と表現していたようです。
やがて,インドで発明されたアラビア数字(現在私たちが使っている数)がヨーロッパに伝わり,小学校で習うような筆算が広まり,計算技術は大きく発展していきました。
インドでは随分早くから「何もない」状態を「0」と表現する発想があり,「0」も数の1つであると認識されていました。
はっきりした時期は分かりませんが,インドでのこの認識こそが,「0の発明」と呼べるものだと言われています。
現在でもインドの計算能力の高さは有名ですが,古来から数に対する感覚の深さがあったのだと思います。
「何もない」を「0がある」と発想転換することで,計算技術に大きな革新をもたらしたわけですから,特にヨーロッパにおいては「計算革命」と呼べるものかもしれません。
 |
インドの数学 ゼロの発明 ちくま学芸文庫 / 林隆夫 【文庫】 価格:1,430円 |
![]()
5 「ゼロ」の発明による,新たな「問題点」
0が発明されたことにより,数の世界は大きく変わりました。
まず,位取り(1の位,10の位・・・)の発想が生まれたことで,これまで分数で表していたものを小数で表せるようになりました。
小数は分数に比べて直感的に分かりやすく,計算も便利なため,あっという間に世界中に広まりました。
また,0は数の世界に革命的な拡張をもたらしました。
0を基準として,正の数,負の数という発想が生まれたのです。
-3,-4,-5といった負の数が数として認知されたのも,0が発明された結果です。
これまではただの「無」という状態に過ぎず,数直線の端に置かれていた0は,負の数の登場により全ての数の基準・中心的存在になったのです。
0にまつわるエピソードは尽きません。
「0を加えてもひいても,何も変化しない」「0をかけると何もかもが0になる」「何かを0で割ることはできない」などのように,0は独特の世界を持っています。
以前,拙稿「0で割るとはどういうこと?」でもお話ししましたが,0にまつわる不思議な話(厄介な問題点)は尽きません。
その「問題点」は,無限や極限を扱う解析学,数論や代数学,特異点等を扱う幾何学等の高等数学の発展にも寄与していたりするそうです。
 |
数の不思議 魔方陣・ゼロ・ゲマトリア (アルケミスト双書) [ ミランダ・ランディ ] 価格:1,320円 |
![]()
最後に1つ問いかけをして終わりたいと思います。
高校数学に通じる方なら「0を何乗しても0」,「何を0乗しても1」というのをご存知ですね。
では,0の0乗はいくらでしょうか?
「何もない状態を,何も掛けない」
という,まさに禅問答のような問いかけですが,果たして・・・



コメント